how to find what percent of a number something is
Lesson 29
Percent OF A NUMBER
Every statement of percentage involves three numbers. For example,
eight is l% of xvi.
8 is chosen the Amount. 50% is the Per centum. 16 is called the Base. The Base of operations e'er follows "of." What you see above is the standard form of any statement of percent.
The Amount is some Percent of the Base.
In a percent problem, we are given ii of those numbers and nosotros are asked to notice the 3rd. We have already seen how to solve any percentage problem with a estimator. The same procedures employ in a written adding, in which we would typically modify the percent to a decimal.
In Lesson 4 nosotros saw how to take 1% and x% of a number but past placing the decimal betoken. Those should be bones skills. What is more, from 1% we can summate 2%, 3%, and so on. While from 10% nosotros tin can hands calculate twenty%, 30% and whatever multiple of 10%.
In Lesson 28 we saw how to solve percent problems by understanding that a percent is a ratio. Here, we volition continue those problems -- we volition see how to detect the Amount with a minimum corporeality of writing. And in Department 3 we volition see how to find the Base.
We begin with the elementary question:
| ane. | How much is any percent of 100? |
| 32% of 100 = ? | |
| Whatever pct of 100 is that number. | |
32% of 100 is 32. 87.ix% of 100 is 87.9. 416% of 100 is 416. For as nosotros saw in Lesson 4,percent is an abridgement for the Latin per centum, which means for each 100. (Per ways for each.) A percent is a number of hundredths.
Case 1. A store paid $100 for a jacket. It then raised the selling price by 28%. But a week later it reduced that cost by 10%. What was the terminal selling cost?
Solution. 28% of $100 is $28. And so the selling price became $128.
10% of that is $12.fourscore. (Lesson 4.)
To subtract $12.80 from $128, round information technology off to $13:
$128 − $13 = $115,plus $.twenty is $115.20.
That was the final selling price.
| two. | How can we observe 25% or a fourth of a number? |
| Take one-half of fifty%. That is, take half of half. | |
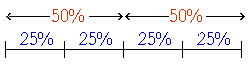
25% is half of fifty%.
Compare Lesson xvi.
Instance 2. How much is 25% of 60?
Answer. One-half of 60 is 30. One-half of 30 is xv.
Example 3. How much is 25% of 180?
Answer. One-half of 180 is ninety. Half of 90 is 45.
Example 4. How much is 25% of 112?
Answer. One-half of 112 = Half of 100 + Half of 12 = 56.
Answer.One-half of 56 = Half of 50 + Half of 6 = 25 + 3 = 28.
Answer.Lesson xvi.
Example five. How much is 25% of $nine.60?
Answer. One-half of $nine.60 = $4.50 + $.30 = $4.fourscore. Half of $four.80 = $ii.40
Example half-dozen. Eighths. How much is 37.5% of $600?
Answer. Upon recognizing that 37.v% means three eighths (Lesson 24), this is not a difficult trouble.
(The pupil should know the eighths; they come oft.)
First, a quarter of $600 is half of $300: $150. And an 8th is one-half of a quarter: $75. Therefore 3 eighths are 3 times $75: $225.
Equivalently, one quarter -- $150 -- is ii eighths. Therefore, three eighths will be one quarter plus one-half of i quarter: $150 + $75 = $225.
| iii. | How can we find fifteen%? |
| Take ten% and add half. | |
Example vii. How much is fifteen% of $70??
| Answer. xv% | = | 10% + Half of 10% |
| = | $seven.00 + $3.50 | |
| = | $10.50. | |
Run into Lesson 4, Question 7: How can nosotros take ten%?
Example 8. If you tip at the rate of 15%, and the bill is $40, how much do you get out?
| Answer. 15% | = | 10% + Half of 10% |
| = | $4.00 + $ii.00 | |
| = | $6.00. | |
In general:
| 4. | How tin can we detect the Amount when nosotros know the Base and the Percent? |
| Amount = Base × Percentage or Percentage × Base of operations | |
Nosotros saw this in Lesson 10 and in Lesson 14.
Example 9. Percent to a decimal. How much is 11% of $420?
Solution 1. eleven% is xi hundredths, which nosotros can represent every bit the decimal .xi. Therefore,
11% of $420 = .xi × 420.
(Lesson 27.) At present,
11 × 420 = ivtwo00 + 420 = four6twenty. (Lesson ix)
Therefore, on separating two decimal digits (Lesson 10),
11% of $420 = $46.twenty.
(Compare Lesson x, Question iv.)
Solution ii. More simply, since eleven% = 10% + 1%, and so
Case x. How much is 30% of $48?
Solution. The educatee should realize that xxx% is only three times 10% and so will always involve multiplication past 3. (Its decimal is .three.)
Now, ten% of $48 is $four.80. Therefore, xxx% is
| 3 × $4.80 | = | 3 × $4 + 3 × $.fourscore |
| = | $12 + $2.40 (Lesson 9) | |
| = | $14.xl. | |
See Lesson nine, The distributive holding of multiplication, Examples 5 and 6.
Instance 11. How much is 40% of $90?
Solution 1. 4 times 9 is 36. 40% of $90 is $36.
Solution two. 10% of $90 is $ix. Therefore xl% is 4 times $nine: $36.
Case 12. Vanessa is nigh to withdraw $3000 from her retirement account. But 20% will exist withheld for taxes. How much volition she actually receive?
Solution. Since twenty% volition exist withheld, she volition receive fourscore%. (The whole is 100%.) fourscore% of $3000 is
.8 × 3000 = 2400.
(Lesson ten. The 0 of .80 is unnecessary. Lesson 3.)
She volition receive $2400.
Example 13. How much is 80% of $45?
Solution 1. If nosotros multiplied by .eight, the answer would take ane decimal digit.
| .8 × 45 | = | 45 × .8 |
| = | 4.5 × 8. | |
For it is easy to do four.5 × 8, that is -- Four and a half times 8.
"Four times 8 is 32. Half of 8 is iv. 32 plus four is 36."
80% of $45 is $36.
(Compare Lesson 27, Multiplying by numbers ending in 5.)
Solution 2. fourscore% means four fifths; 45 has an exact fifth part. Therefore we can reason as follows:
One fifth of 45 is 9. Therefore four fifths are four 9'southward -- 36.
Example 14. How much is 75% of 108?
Answer. We could write 75% as the decimal .75, and then multiply
.75 × 108.
Even so, 75% is three quarters. Therefore we could calculate
Three quarters of 108.
That is not difficult if we decompose 108 into 100 + viii.
| 3 quarters of 108 | = | Three quarters of 100 + Iii quarters of 8 | |
| = | 75 + 6 | (Lesson 15) | |
| = | 81. | ||
75% of 108 is 81.
Example 15. How much is 18.ix% of $314?
Respond. Use your calculator![]() Press 314 × eighteen.9%. Encounter 59.346, which is approximately $59.35.
Press 314 × eighteen.9%. Encounter 59.346, which is approximately $59.35.
To exercise a problem in writing, and so, we must limited the percent either every bit a decimal or a fraction. Equally for expressing a percent as a fraction:
| v. | How tin we stand for a percent as a fraction? |
| 29% = ? | |
| Nosotros can represent a pct every bit a fraction whose denominator is 100. That will sometimes atomic number 82 to a whole number or a mixed number. | |
Examples xvi.
| 29% | = | 29 100 | . | ||||
| threescore% | = | threescore 100 | = | 6 10 | = | 3 v | . (Lesson 22, Question 5) |
| 200% | = | 200 100 | = 2. | ||||
| 250% | = | 200% + 50% = two½. |
| 225% | = | two¼. |
| 233 | 1 3 | % = 2 | i 3 | . |
In addition, the student should know:
| 12.5% | = | 1 viii | . ( | ane viii | is half of | ane 4 | , which is 25%. ) |
| Lesson 24 | |||||||
| 37.5% | = | iii 8 | , 62.five% = | 5 8 | , 87.5% = | vii viii | . |
Example 17. How much is 250% of 32?
Answer. 250% = 2½.
| 2 ½ × 32 | = | 2 × 32 +½ × 32 |
| "Two times 32 +Half of 32" | ||
Lesson 27, Question 2.
Instance xviii. How much is 37½% of $twoscore?
| Answer. 37½% = | 3 8 | . (Lesson 24).)One eighth of $40 is $v. |
Therefore, three eighths are three × $v = $15.
| Example 19. Thirds. | How much is 33 | one 3 | % of 720? |
| How much is 66 | 2 3 | %? | |
| Answer. 33 | ane 3 | % means a third. (Lesson 16.) To take a third |
of 720, nosotros can decompose information technology into multiples of 3 as follows:
720 = 600 + 120.
A 3rd of 600 is 200.
A third of 120 is 40.
Therefore a third of 720 is 240.
| Equally for 66 | ii 3 | %, information technology means ii thirds.One tertiary of 720 |
is 240.
Therefore 2 thirds are 2 × 240 = 480.
| Case twenty. Calculator problem. How much is 66 | 2 three | % |
of $76.27?
Solution. To find two thirds, we must start find 1 third, and then multiply past 2. Press
| seven | half-dozen | . | 2 | vii | ÷ | three | = | × | two | = |
Encounter
This is approximately $l.85.
The standard textbook method for finding a pct of a number, has been to alter the percent to a decimal and multiply. So to find 24% of $412, we are taught to alter 24% to the decimal .24 (Lesson 4), and multiply times 412.
But is anyone with a calculator going to do that these days? And aren't there more important things to learn virtually percent? Like how to accept 25% of $412 without writing anything! Take half of 50%, which is $206. 25% is $103.
24% of $412 volition and so be 25% − 1%:
| 103 − 4.12 | = | 103 − three − 1 − .12 |
| = | 100 − 1 − .12 | |
| = | 99 − .12 | |
| = | $98.88. | |
| Example 21. fourteen is 66 | 2 3 | % of what number? |
Respond. Here, the Base is missing, the number that follows of. This is Instance ii in Section 3.
At this point, please "turn" the page and do some Problems.
or
Continue on to the Section two: Partial percent
First Lesson on Percentage.
Introduction | Habitation | Table of Contents
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: instructor@themathpage.com
Source: https://themathpage.com/Arith/percent-of-a-number.htm
0 Response to "how to find what percent of a number something is"
Post a Comment